Our Paper Multi-Class Hypersphere Anomaly Detection (MCHAD) has been accepted for presentation at the ICPR 2022. In summary, we propose a new loss function for learning neural networks that are able to detect anomalies in their inputs.
Poster for MCHAD (PDF).
MACHAD is available via pytorch-ood. You can find example code here.
How does it work? §
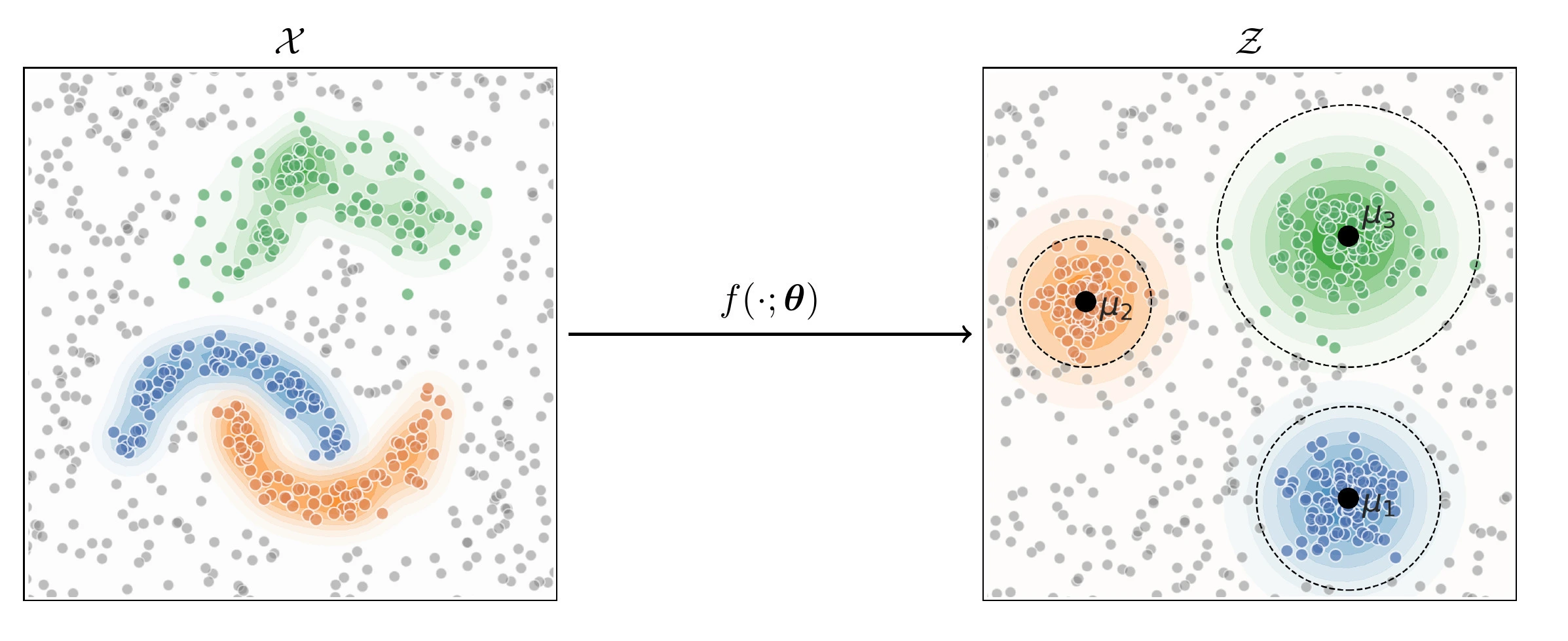
The general idea is that we want a neural network $f_{\theta}: \mathcal{X} \rightarrow \mathcal{Z}$ that maps inputs from the input space to some lower dimensional representation in such a way that points from class $y$ cluster around a hypersphere with center $\mu_y$ in the output space. Because the neural network can learn non-linear functions, the classes in the input space can have arbitrarily complex shapes.
To train this neural network, we optimize its parameters $\theta$ to minimize a loss function. We then hope that the model only maps points from the known classes into the spheres of the corresponding spheres, while other points that are dissimilar to the training data (i.e., anomalies) are mapped further away because the model never learned to map these points close to the centers.
Omitting some details, the loss function we propose has three different components, each of which we will explain in the following.
Intra-Class Variance §
We want the representations $f(x)$ of one class to cluster as tightly around a class center $\mu_y$ as possible. For this, we can use the Intra class variance loss, which is defined as:
$$ \mathcal{L}_{\Lambda}(x,y) = \Vert \mu_y - f(x) \Vert^2 $$
Inter-Class Variance §
A trivial solution to minimize $ \mathcal{L}_{\Lambda}$ would be to map all inputs to the same point, which would lead to the collapse of the model. To prevent this, we have to add a second term that ensures that the points remain separable:
$$ \mathcal{L}_{\Delta}(x,y) = \log \left( 1 + \sum e^{ \Vert \mu_y - f(x) \Vert^2 - \Vert\mu_j - f(x) \Vert^2} \right) $$
This expression might seem somewhat random, but it can, in fact, be derived from the method of maximum likelihood.
MCHAD on CIFAR 10
Extra-Class Variance §
Sometimes, we have a set of example outliers at hand. Previous work showed that the robustness of models can be significantly improved by including these in the optimization. Therefore, we can add a term that incentivizes such outliers to be mapped sufficiently far away from the class centers:
$$ \mathcal{L}_{\Theta}(x) = \max \lbrace 0, r_y^2 - \Vert \mu_y - f(x) \Vert^2 \rbrace $$
where $x$ is some outlier and $r_y$ is some class conditional radius. This term can also be applied to other methods that aim to learn spherical clusters in their output space. We refer to it as Generalized MCHAD.
Generalized MCHAD on CIFAR 10
How well does it work? §
Our experiments found that both MCHAD and Generalized MCHAD outperform other hypersphere learning methods. In ablations studies, we also investigated the influence of each of the loss terms and demonstrated that all of them contribute to the overall performance regarding discriminative power on normal data and the ability to detect anomalies.
